Ganzrationale Funktionen
Symmetrie

Alle diese Dinge haben einen Punkt oder eine Achse, an denen man sie spiegeln kann.
Auch in der Mathematik begegnet uns die Symmetrie häufig. Heute wollen wir dir alles zur Symmetrie ganzrationaler Funktionen zeigen und sie dir mit einfachen Beispielen und abschließenden Übungsaufgaben näher bringen.
- Exponenten gerade: Symmetrie zur y-Achse
- Exponenten ungerade: Symmetrie zum Ursprung
Das erwartet dich
Unser Inhaltsverzeichnis
Was ist Symmetrie


Genau das beschreibt Symmetrie. Es ist vollkommen ausreichend, die Hälfte einer symmetrischen Figur zu kennen, wenn man die andere ergänzen möchte - man spiegelt sie einfach!

Symmetrie am Graphen
Ganzrationale Funktionen lassen sich - bezogen auf die Symmetrie - in 3 Gruppen einteilen:- symmetrisch zur y-Achse
- symmetrisch zum Ursprung
- keine einfache Symmetrie
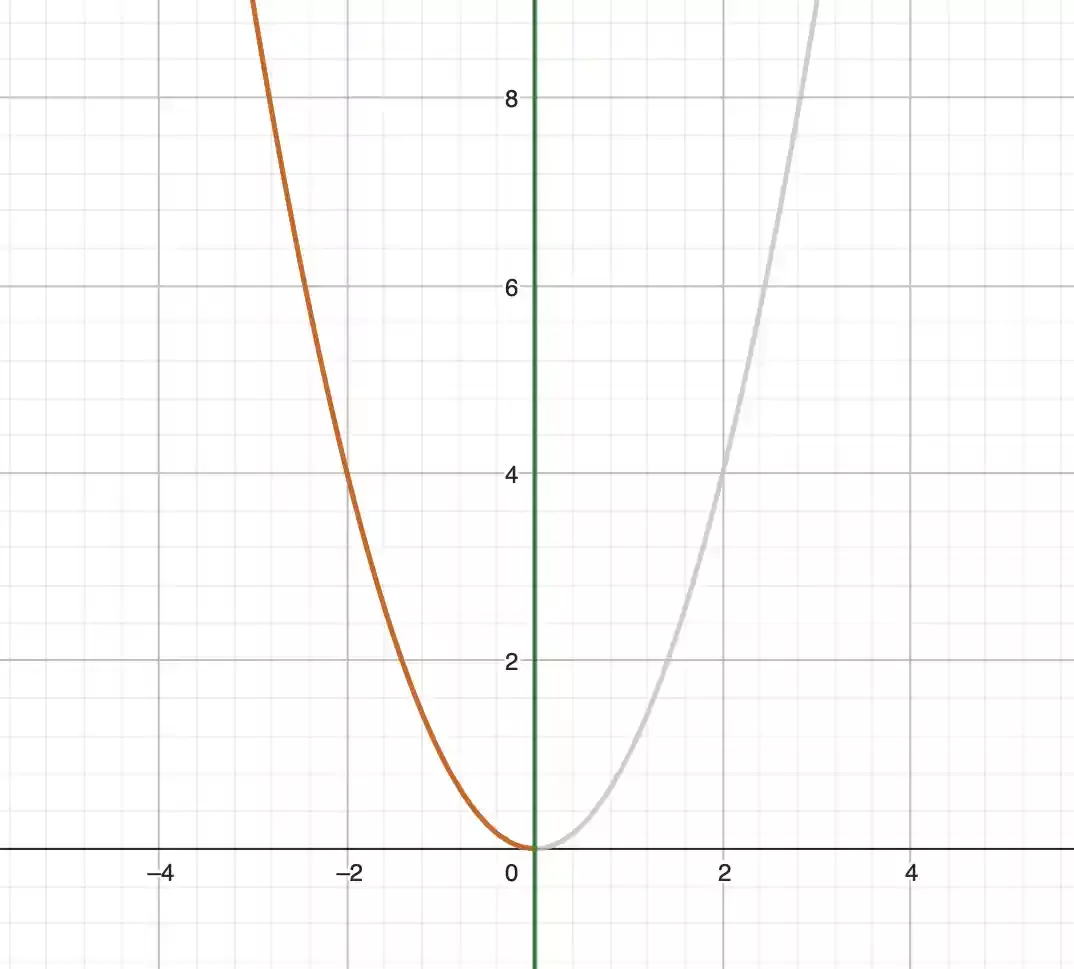

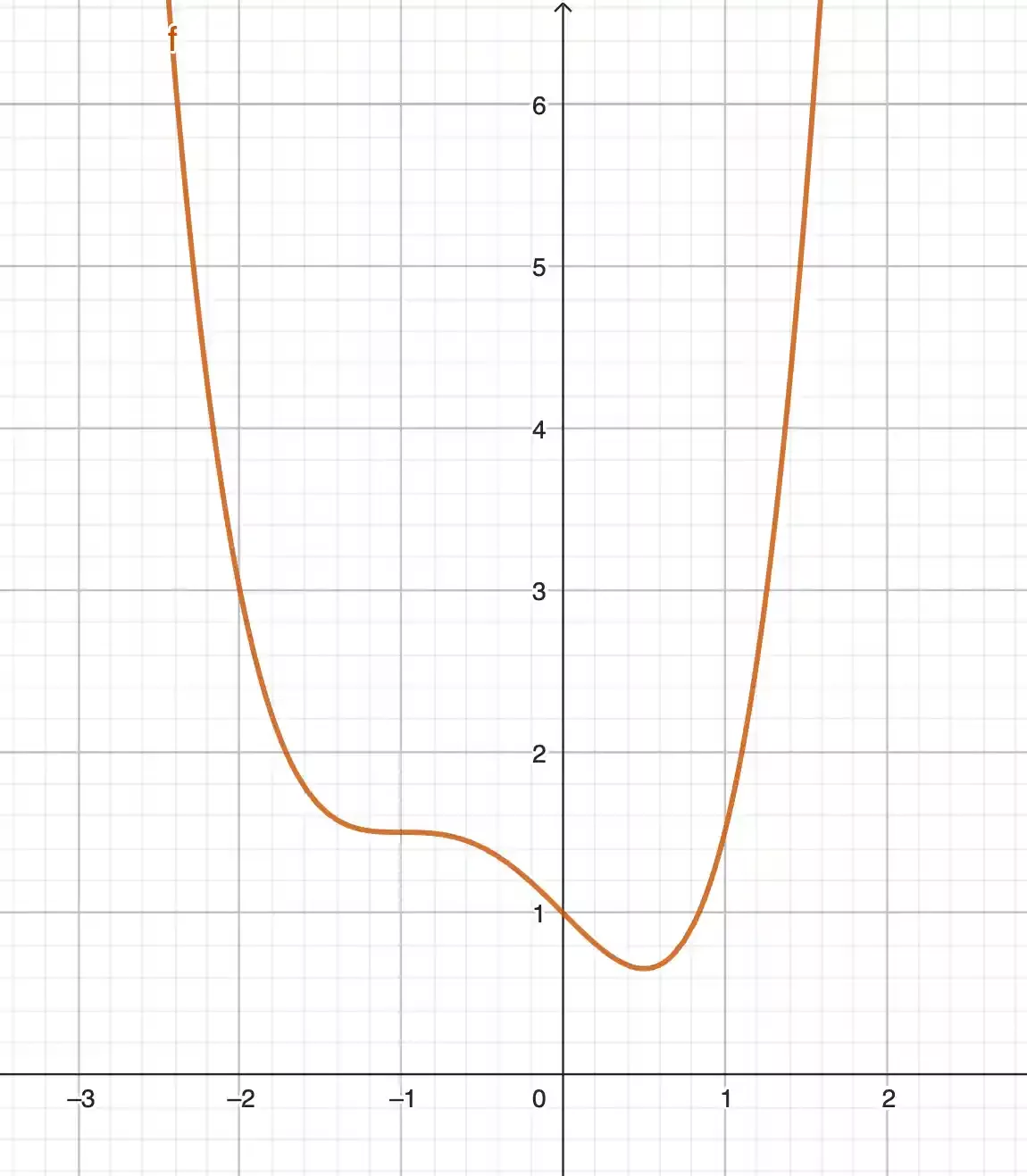
Kannst du an diesen Stellen keinen Spiegel ins Koordinatensystem legen, liegt keine einfache Symmetrie vor.
Symmetrie an der Funktionsgleichung erkennen
Du weißt jetzt, wie man Symmetrie am Graphen erkennt und welche Arten von Symmetrie wir voneinander unterscheiden können. Aber was, wenn es keinen Graphen gibt und du nur die Funktionsgleichung hast, um eine Aussage über die Symmetrie des Graphen zu treffen?Schauen wir uns das Beispiel einmal an:
- gerade→ Symmetrie zur y-Achse
- ungerade→ Symmetrie zum Ursprung
- gemischt→ keine einfache Symmetrie

Aufgaben
Übung : Bestimme die Symmetrie der folgenden ganzrationalen Funktionen\( x \)
| 1. \( f(x) = 3x-2\) | 2. \( g(x) = 2x^2+4 \) |
| 3. \( h(x) = 4x^5-3x^3+x\) | 4. \( i(x) = 5x^4-3x^2+2x-5\) |
| 5. \( j(x) = 2x^7-x^5+x\) | 6. \( k(x) = 5x^4-8x^2+7\) |
Lösungen
Übung : Bestimme die Symmetrie der folgenden ganzrationalen Funktionen\( x \)
| 1. keine einfache Symmetrie | 2. Symmetrie zur y-Achse |
| 3. Symmetrie zum Ursprung | 4. keine einfache Symmetrie |
| 5. Symmetrie zum Ursprung | 6. Symmetrie zur y-Achse |
Ab hier findest du weiterführende Informationen zur Symmetrie ganzrationaler Funktionen
Symmetrie ganzrationaler Funktionen
Symmetrie ist ein faszinierendes Konzept, das auch in der Welt der ganzrationalen Funktionen eine wichtige Rolle spielt. Ganzrationale Funktionen, also Funktionen, die nur aus Ganzzahlen und positiven Potenzen von x bestehen, können besondere symmetrische Eigenschaften aufweisen. Diese Symmetrien helfen nicht nur dabei, das Verhalten der Funktion besser zu verstehen, sondern auch dabei, komplexe Berechnungen zu vereinfachen und graphische Darstellungen zu interpretieren.
Wenn du die Symmetrie einer ganzrationalen Funktion untersuchen möchtest, stellt sich die Frage, ob die Funktion achsensymmetrisch oder punktsymmetrisch ist. Diese Symmetrien können dir viel über das Verhalten der Funktion sagen und sind daher von zentraler Bedeutung in der Mathematik, besonders bei der Analyse von Graphen.
Achsensymmetrie
Eine Funktion hat dann eine Achsensymmetrie, wenn sie sich bei einer Spiegelung an der y-Achse nicht verändert. Das bedeutet, dass der Graph der Funktion auf der linken Seite der y-Achse genauso aussieht wie auf der rechten Seite. Dies ist besonders bei Funktionen der Fall, die nur gerade Potenzen von x enthalten. Ein Beispiel hierfür wäre eine quadratische Funktion, deren Graph eine Parabel ist, die entlang der y-Achse gespiegelt wird.
Punktsymmetrie
Eine Funktion besitzt Punktsymmetrie, wenn sie bei einer Drehung um den Ursprung um 180 Grad ihren Graphen auf sich selbst abbildet. Das heißt, für jede Stelle auf dem Graphen gibt es einen symmetrischen Punkt, der denselben Abstand zum Ursprung hat, aber in die entgegengesetzte Richtung zeigt. Ganzrationale Funktionen, die nur ungerade Potenzen von x enthalten, zeigen oft punktsymmetrisches Verhalten. Ein klassisches Beispiel hierfür ist die Funktion x³, deren Graph eine typische Kurve bildet, die sowohl nach oben als auch nach unten hin symmetrisch zum Ursprung verläuft.
Die Rolle der Potenzen
Die Symmetrie einer ganzrationalen Funktion lässt sich oft durch die Potenzen der einzelnen Terme in der Funktion erklären. Wenn alle Exponenten gerade sind, wird die Funktion achsensymmetrisch zur y-Achse sein. Wenn alle Exponenten ungerade sind, weist die Funktion Punktsymmetrie zum Ursprung auf. In komplexeren Fällen, wenn sowohl gerade als auch ungerade Potenzen vorkommen, kann es sein, dass die Funktion keine vollständige Symmetrie aufweist, aber trotzdem Teilaspekte wie Achsensymmetrie oder Punktsymmetrie zeigen kann.
Anwendung der Symmetrie in der Praxis
Das Verständnis der Symmetrie einer Funktion ist nicht nur für die theoretische Mathematik wichtig, sondern hat auch zahlreiche praktische Anwendungen. In der Physik, beispielsweise, hilft die Symmetrie dabei, bestimmte Probleme zu lösen, bei denen die Eigenschaften eines Systems in Bezug auf bestimmte Achsen oder Punkte unverändert bleiben. Auch in der Ingenieurwissenschaft ist Symmetrie ein wichtiges Konzept, um die Eigenschaften von Bauteilen oder mechanischen Systemen zu analysieren und zu optimieren.
Tipps zur Identifizierung von Symmetrien
Um die Symmetrie einer ganzrationalen Funktion zu erkennen, sollte man die Funktion genau analysieren und auf die Exponenten der einzelnen Terme achten. Eine schnelle Möglichkeit zur Identifikation ist das Testen von Werten für x, sowohl für positive als auch für negative x-Werte. Wenn die Werte auf beiden Seiten des Ursprungs oder der y-Achse gleich sind, handelt es sich um eine Symmetrie.
Mit Übung und den richtigen mathematischen Werkzeugen kannst du die Symmetrie von Funktionen schnell und sicher erkennen und sie für weitergehende Berechnungen und Analysen nutzen.
Alle Fragen auf einen Blick - unser FAQ
Damit keine Frage mehr offen bleibt
Weitere Artikel aus unserem Blog

Ableiten: Faktor- und Summenregel
Entdecke jetzt, wie leicht Ableiten sein kann!...

Symmetrie
In deinem Alltag begegnen dir oft symmetris...

Rechteck - Umfang & Flächeninhalt
In unserem Alltag begegnen uns überall Rechtecke:...

Musik als effektive Unterstützung beim Lernen
Warum Musik beim Lernen hilfreich sein kann Musik...

Die wichtigsten Ableitungsregeln
Wenn du eine Übersicht aller Ableitungsregeln br...