Rechtecke verstehen
Rechteck - Umfang & Flächeninhalt
Einleitung
Immer wieder wirst du die Fläche, oder den Umfang solcher Rechtecke bestimmen müssen. Zum Glück ist das gar nicht so schwer! Anhand einfacher Beispiele zeigen wir dir, wie es funktioniert. Am Ende des Beitrags findest du außerdem Übungsaufgaben, mit denen du dein neues Wissen testen kannst.
Den Umfang berechnen
Was versteht man eigentlich unter Umfang?
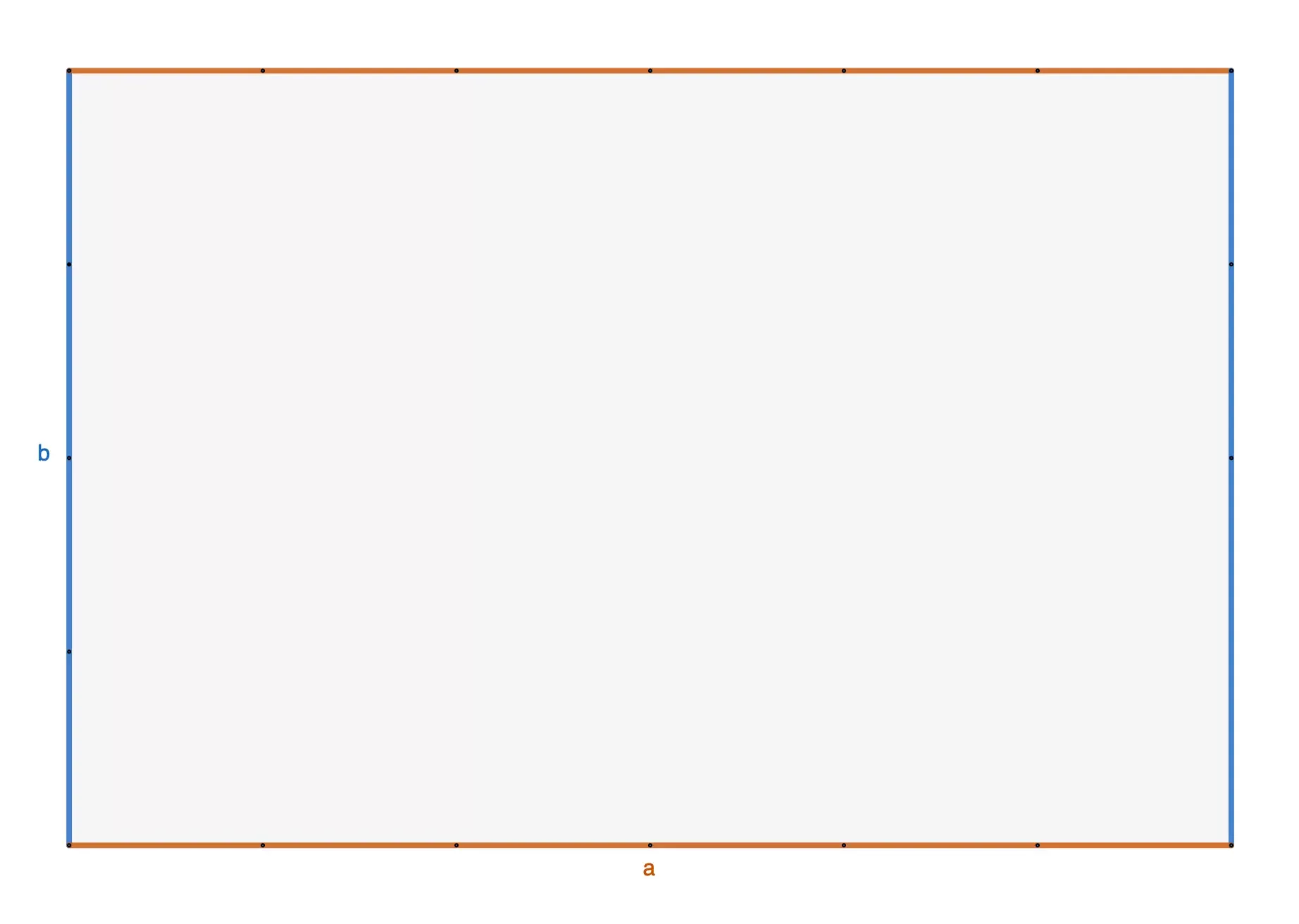
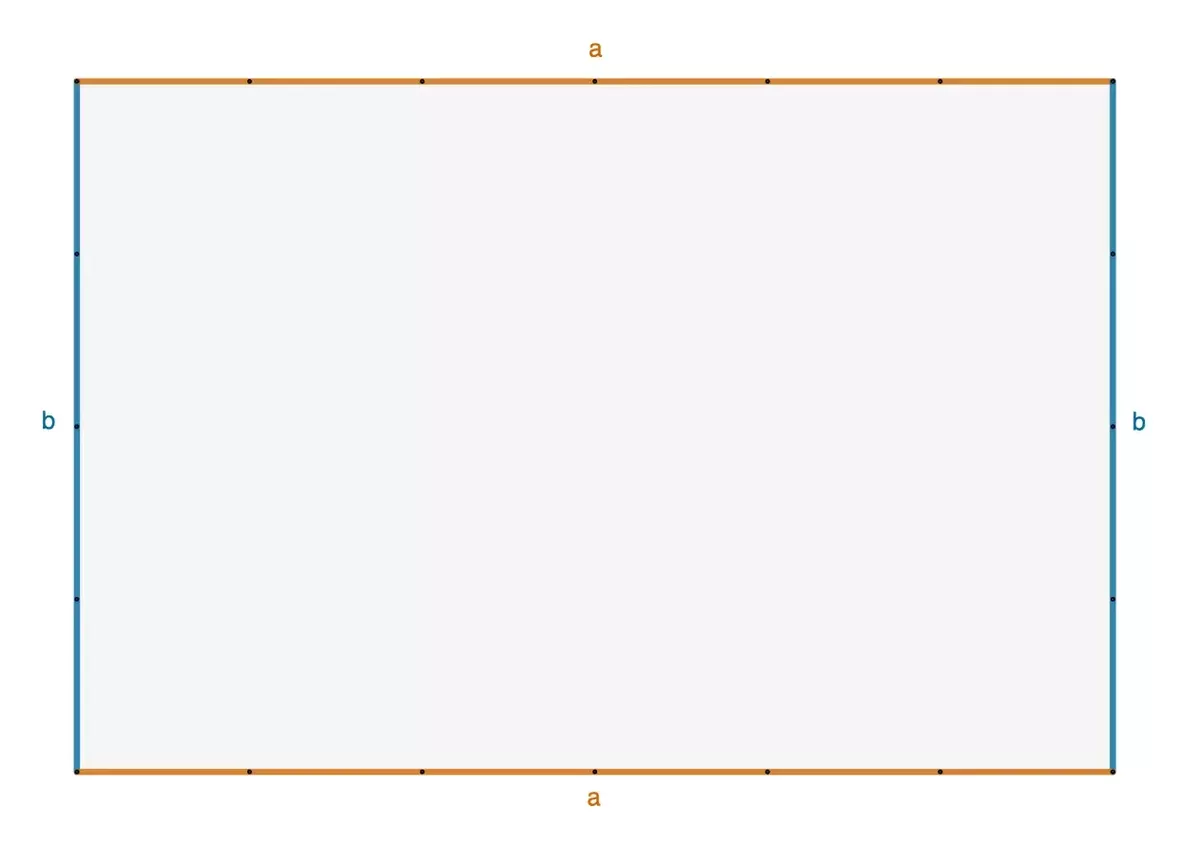
Der Umfang einer Figur ist die Strecke, die du zurücklegst, wenn du einmal vollständig um die Figur herumgehst. In dem Rechteck, das du hier siehst, ist diese Strecke - der Umfang - in Grün dargestellt.
Um den Umfang zu berechnen, addierst du einfach alle 4 Seiten. Schauen wir uns an einem Beispiel an, wie das funktioniert.
Wenn der Umfang gegeben ist
Jetzt können wir die \(10\) auf die andere Seite der Gleichung ziehen:
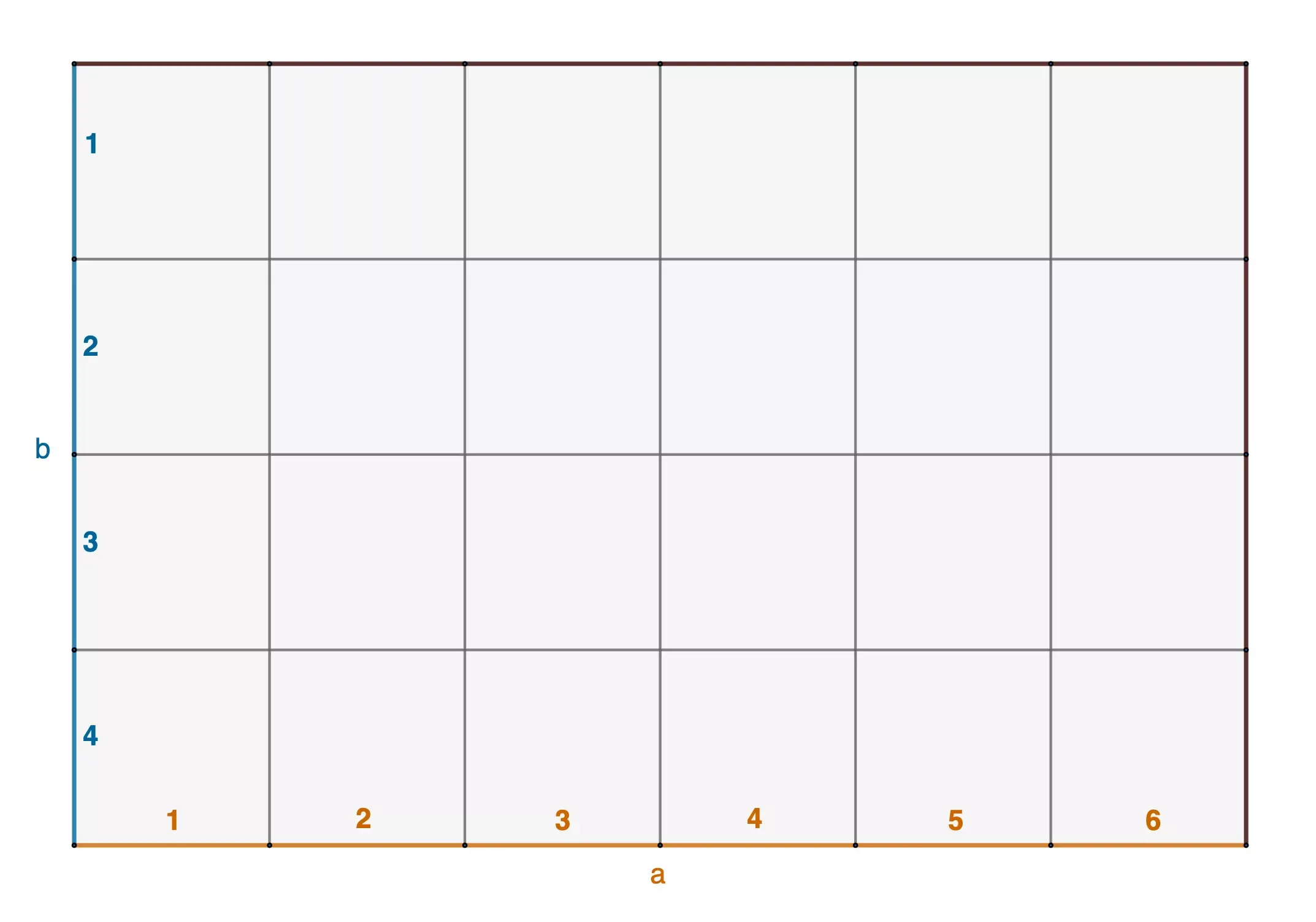
Den Flächeninhalt berechnen
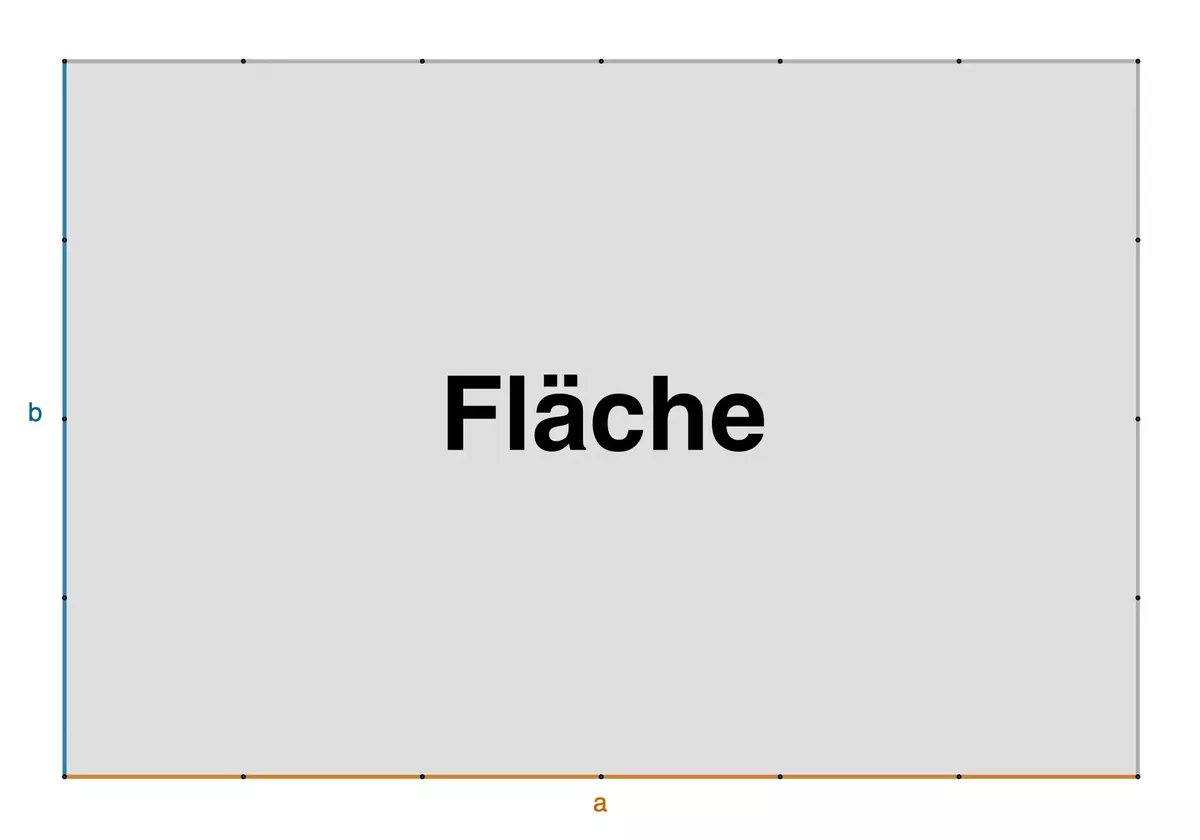
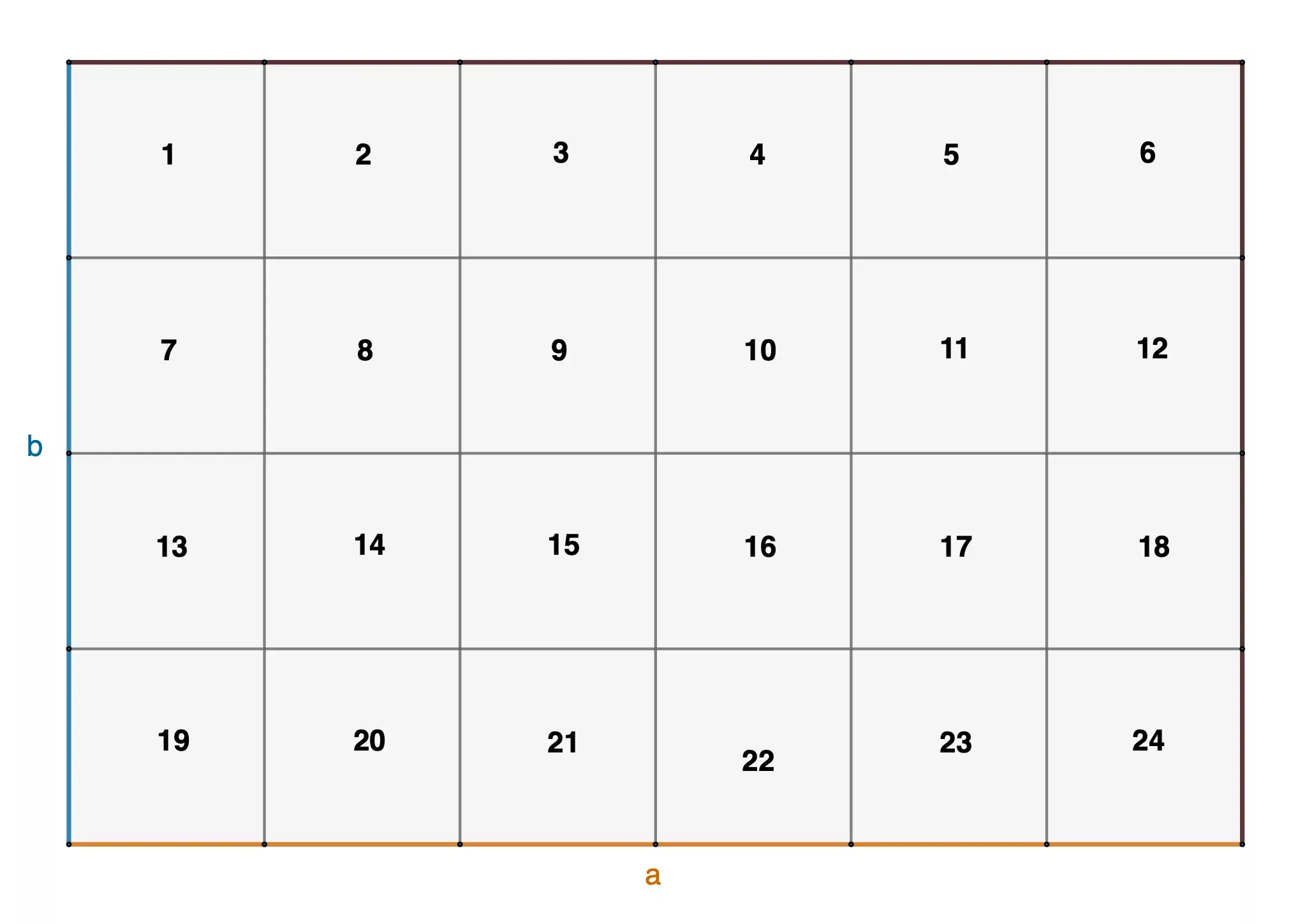
Jedes Kästchen ist einen Zentimeter lang und breit.
Das Rechteck hat somit einen Flächeninhalt von \(24cm^2\).
Wenn der Flächeninhalt gegeben ist
Teste dein Wissen
Übungen
Bestimme die fehlenden Angaben - achte auf die Einheit.
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
Was ist der Unterschied zwischen Umfang und Fläche eines Rechtecks?
Der Umfang beschreibt die Länge des Randes des Rechtecks, während die Fläche den gesamten Raum angibt, den das Rechteck bedeckt.
Wie kann ich den Umfang eines Rechtecks berechnen?
Addiere die Länge und die Breite des Rechtecks und multipliziere das Ergebnis mit zwei.
Wie wird die Fläche eines Rechtecks berechnet?
Multipliziere die Länge mit der Breite, um die Fläche zu erhalten.
Gibt es Besonderheiten beim Rechteck gegenüber anderen Formen?
Ja, ein Rechteck hat immer vier rechte Winkel und gleich lange gegenüberliegende Seiten, was die Berechnungen vereinfacht.
Warum ist das Wissen über Umfang und Fläche eines Rechtecks wichtig?
Dieses Wissen hilft, Platzbedarf, Materialverbrauch und Kosten in verschiedenen Bereichen des Alltags und der Arbeit besser zu planen.
Vertiefung
Weiterführende Informationen
Das Rechteck als grundlegende geometrische Form
Das Rechteck ist eine der bekanntesten und am häufigsten verwendeten Formen in der Geometrie. Ob in Bauplänen, Designprojekten oder mathematischen Berechnungen – das Rechteck begegnet uns überall. Es zeichnet sich durch seine einfache Struktur aus: vier rechte Winkel und parallele gegenüberliegende Seiten. Dieses geometrische Grundelement bietet dir die Möglichkeit, Flächen und Umfänge präzise zu berechnen. Indem du die Eigenschaften eines Rechtecks verstehst, kannst du nicht nur mathematische Aufgaben lösen, sondern auch praktische Anwendungen in deinem Alltag meistern, wie das Auslegen eines Fußbodens oder das Berechnen von Materialkosten. In diesem Beitrag erfährst du alles Wissenswerte zu Umfang und Fläche eines Rechtecks, ergänzt durch Tipps und häufige Fehler, die du vermeiden solltest.
Die mathematische Bedeutung
Umfang und Fläche eines Rechtecks spielen eine zentrale Rolle in vielen Bereichen der Mathematik und der realen Welt. In der Algebra hilft die Rechtecksfläche bei der Visualisierung quadratischer Terme. In der Praxis wird der Umfang beispielsweise für den Zuschnitt von Materialien oder die Einzäunung eines Grundstücks verwendet, während die Fläche in Anwendungen wie Bodenbelägen oder Bauprojekten wichtig ist.
Häufige Fehler vermeiden
- Seiten vertauschen: Ein häufiger Fehler ist, die Seitenlängen a und b falsch zuzuordnen.
- Formeln falsch anwenden: Manche verwechseln die Formeln für Umfang und Fläche. Achte darauf, dass beim Umfang die Summe der Seiten multipliziert wird, während bei der Fläche die Seitenlängen direkt multipliziert werden.
Tipps für effektives Lernen
Übe, verschiedene Rechtecke mit unterschiedlichen Seitenlängen zu analysieren und berechne deren Umfang und Fläche. Visualisiere die Form, indem du Rechtecke aufzeichnest, und überprüfe, ob die berechneten Werte mit deinen Zeichnungen übereinstimmen. Nutze auch praktische Beispiele, um die Theorie zu festigen.
Die Bedeutung des Rechtecks in der Geometrie
Das Rechteck ist nicht nur ein mathematisches Konzept, sondern auch ein Symbol für Ordnung und Struktur. In Architektur, Kunst und Design bietet es eine einfache, aber kraftvolle Möglichkeit, Formen zu gestalten und Flächen zu organisieren. Das Verständnis von Umfang und Fläche eines Rechtecks ist ein grundlegender Schritt, um die Welt der Geometrie zu erschließen.
