Geometrie im Raum
Der Quader
Einleitung
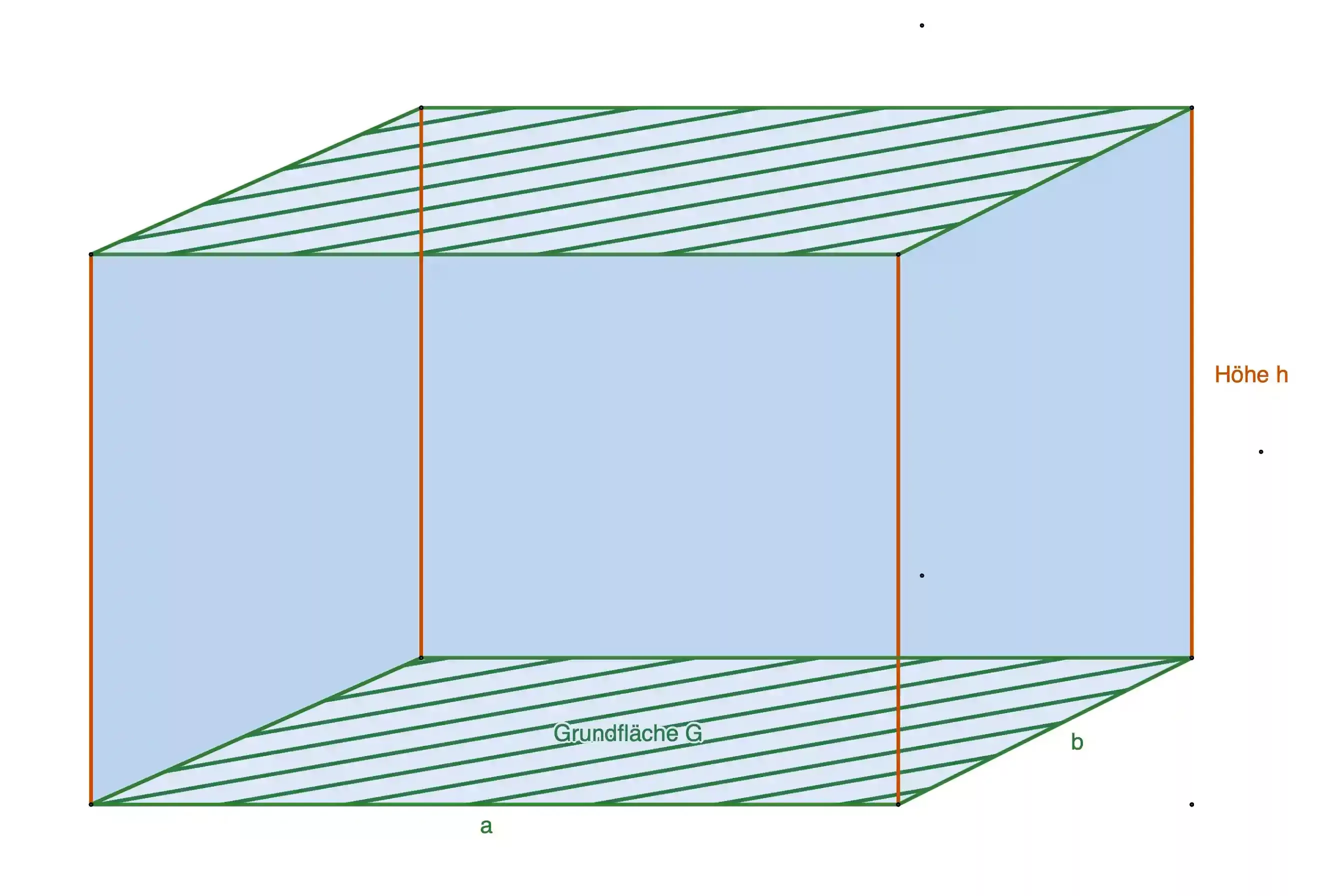
Auch der Raum, in dem du sitzt, ist ein Quader. Ein Quader ist ein Körper, der aus 6 rechteckigen Flächen besteht. Die Flächen, die sich gegenüber liegen, sind jeweils gleich groß und parallel zueinander.
Die Grundfläche des Quaders
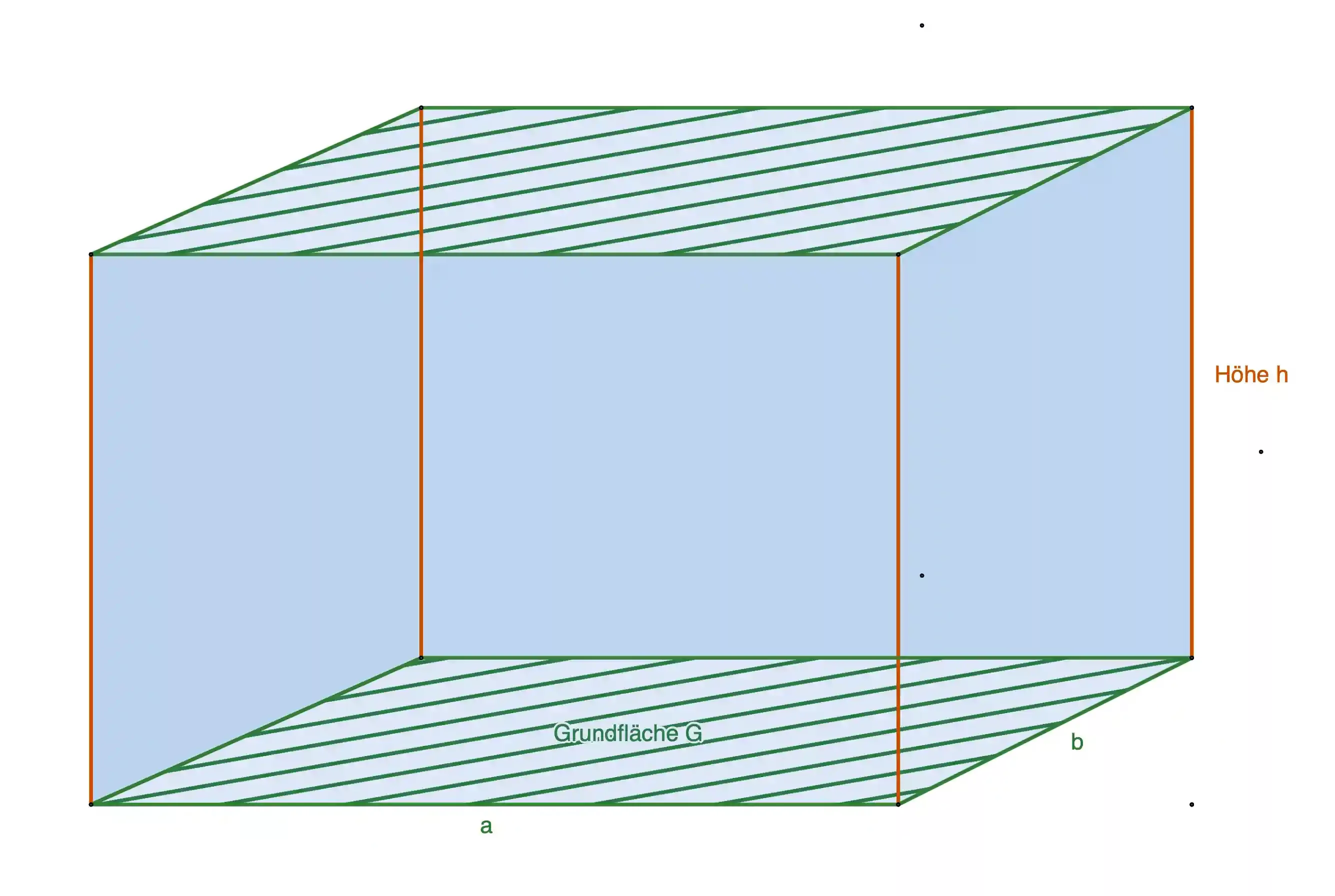
In Formelsammlungen findest du diese Formel. Aber was, wenn die Seiten in deiner Aufgabe nicht a und b, sondern x und y oder Peter und Hugo heißen? Wie rechnest du dann? Es ist immer besser, sich klarzumachen, wie eine Formel aufgebaut ist und sie zu verstehen. Das macht es leichter, sie sich zu merken, und anzuwenden. Merke dir also, dass du den Flächeninhalt eines Rechtecks berechnest, indem du die beiden Seiten, die sich in einer Ecke treffen, miteinander multiplizierst.
Das Volumen eines Quaders
Dazu verwendest du die Formel zur Berechnung der Grundfläche direkt in der Volumenformel.
Die Oberfläche eines Quaders
Wenn du ein Geschenk einpacken möchtest, ist die Oberfläche das Papier, das du benötigst, um es vollständig zu bedecken. Ein Quader ist ein Körper, der aus Rechtecken besteht.
Dabei sind immer die beiden sich gegenüberliegenden Flächen parallel und in ihrer Fläche identisch.
Das nutzen wir zur Berechnung der Oberfläche.
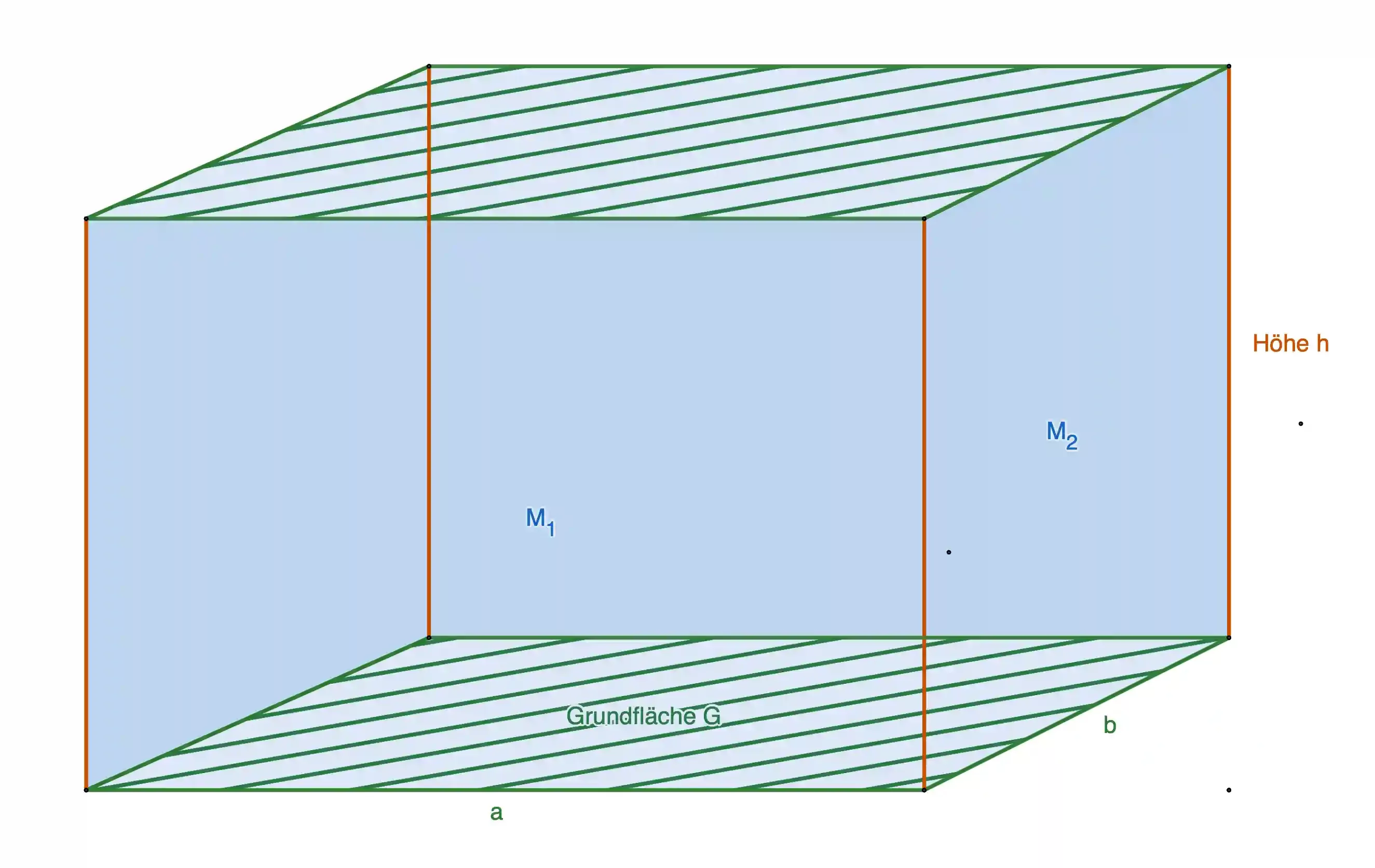
Sie besteht aus 4 Flächen. Vorne und hinten die beiden identischen Flächen \({\textcolor{blue}{M_1}}\), links und rechts die beiden identischen Flächen \({\textcolor{blue}{M_2}}\) . Das bedeutet:
Dazu verwendest du die Formeln zur Berechnung von Grundfläche und Mantelfläche direkt in der Oberflächenformel.
Der Würfel - auch nur ein Quader
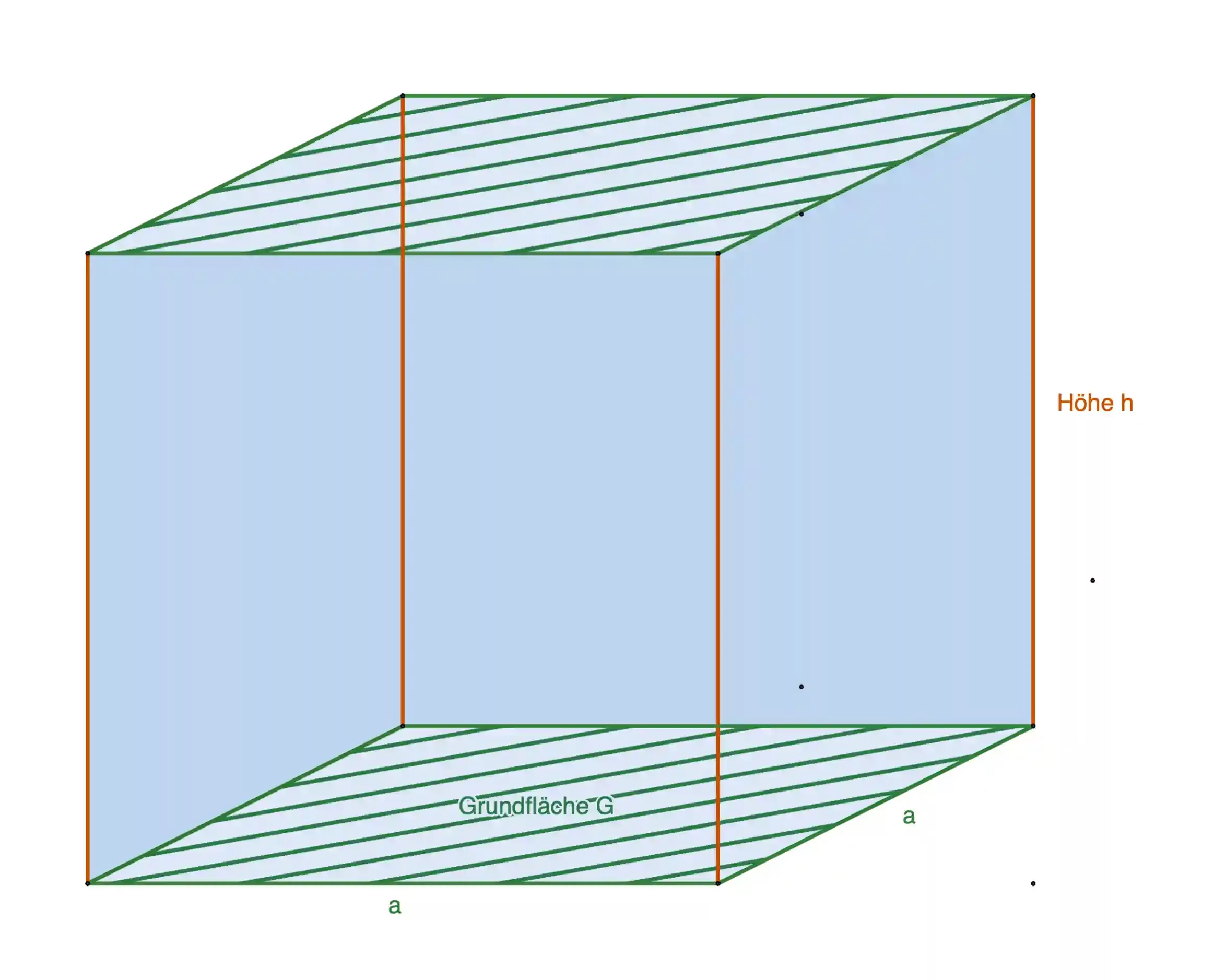
Ein Quader, der aus 6 quadratischen Flächen besteht. Und ein Quadrat ist nichts anderes als ein Rechteck, mit 4 gleich langen Seiten.
Grundfläche
Volumen
Oberfläche
Jetzt machen wir uns zu nutze, dass beim Würfel alle 6 Flächen gleich groß sind:Teste dein Wissen
Übungen
Berechne Volumen und Oberfläche der folgenden Körper.
Löse die folgenden Textaufgaben.
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
Wie berechnet man das Volumen eines Quaders?
Das Volumen eines Quaders wird berechnet, indem man die Länge, die Breite und die Höhe des Quaders miteinander multipliziert.
Wie berechnet man die Oberfläche eines Quaders?
Die Oberfläche eines Quaders wird mit der Formel: Oberfläche = 2 × (Länge × Breite + Länge × Höhe + Breite × Höhe) berechnet. Achte darauf, alle Paare von Flächen korrekt zu addieren.
Was passiert, wenn der Quader eine der Dimensionen (Länge, Breite, Höhe) null hat?
Wenn eine der Dimensionen null ist, hat der Quader kein Volumen und keine Oberfläche, da es sich dann nicht mehr um einen dreidimensionalen Körper handelt.
Kann ein Quader auch als Würfel bezeichnet werden?
Ja, ein Quader ist ein spezieller Fall eines Würfels, wenn alle drei Dimensionen gleich sind. In diesem Fall sind Länge, Breite und Höhe identisch, und die Flächen des Quaders sind gleich.
Warum ist es wichtig, das Volumen und die Oberfläche eines Quaders zu kennen?
Das Volumen hilft dir zu verstehen, wie viel Raum der Quader einnimmt, während die Oberfläche die Fläche beschreibt, die für Beschichtungen, Verpackungen oder den Materialbedarf benötigt wird.
Vertiefung
Weiterführende Informationen
Der Quader als dreidimensionale Form
Der Quader ist eine der grundlegendsten und praktischsten Formen in der Geometrie. Du findest ihn in vielen Bereichen des Lebens – sei es in Form von Möbeln, Kisten oder sogar Gebäuden. Ein Quader ist ein dreidimensionaler Körper, der sechs rechteckige Flächen hat, wobei gegenüberliegende Flächen gleich groß sind. Die Berechnung des Volumens und der Oberfläche eines Quaders ist eine wichtige Fähigkeit, die nicht nur in der Mathematik, sondern auch in der Architektur, im Ingenieurwesen und in der praktischen Lebensgestaltung Anwendung findet.
Was sind Volumen und Oberfläche eines Quaders?
- Das Volumen eines Quaders gibt an, wie viel Raum der Körper einnimmt, und wird mit der Formel berechnet: Volumen = Länge × Breite × Höhe.
- Die Oberfläche eines Quaders beschreibt die Gesamtfläche der äußeren Flächen und wird mit der Formel berechnet: Oberfläche = 2 × (Länge × Breite + Länge × Höhe + Breite × Höhe).
Diese Formeln sind einfach zu verstehen und ermöglichen es dir, die räumlichen Eigenschaften eines Quaders schnell zu berechnen.
Mathematische Bedeutung von Volumen und Oberfläche
Das Volumen eines Quaders hilft dir, den Raum zu verstehen, den der Körper einnimmt – zum Beispiel, wenn du wissen möchtest, wie viel Wasser ein Behälter aufnehmen kann. Die Oberfläche ist besonders wichtig, wenn du die Menge an Material berechnen möchtest, das benötigt wird, um den Quader zu beschichten, wie etwa bei der Bemalung oder beim Verpacken.
Häufige Fehler vermeiden
- Formeln falsch anwenden: Ein häufiger Fehler ist das Verwechseln der Formeln für Volumen und Oberfläche. Achte darauf, dass du beim Volumen nur die Länge, Breite und Höhe multiplizierst und bei der Oberfläche alle Paare von Flächen korrekt addierst.
- Maßeinheiten nicht berücksichtigen: Wenn du mit unterschiedlichen Maßeinheiten arbeitest, stelle sicher, dass du diese vor der Berechnung in dieselbe Einheit umwandelst.
Tipps für effektives Lernen
Es ist hilfreich, den Quader zu visualisieren, um ein besseres Verständnis der Form zu entwickeln. Übe, verschiedene Quader mit unterschiedlichen Längen, Breiten und Höhen zu analysieren und berechne deren Volumen und Oberfläche. Dies hilft dir nicht nur, die Formeln zu verstehen, sondern auch ein praktisches Gefühl für den Quader zu bekommen. Es kann auch sinnvoll sein, praktische Aufgaben zu lösen, wie das Berechnen des Volumens eines Kartons oder das Berechnen der Oberfläche eines Raums.
Die Bedeutung des Quaders in der Geometrie
Der Quader ist eine fundamentale Form in der Geometrie und dient als Grundlage für das Verständnis komplexerer dreidimensionaler Formen. Seine Anwendungen reichen von der Berechnung von Volumen und Oberfläche in der Technik bis hin zur Modellierung von realen Objekten in der Architektur. Das Verständnis der Formeln für Volumen und Oberfläche eines Quaders ist daher ein wichtiger Schritt auf dem Weg, die Welt der dreidimensionalen Geometrie zu beherrschen.
